• 起因

今天在做 leetcode 时遇到一道的题, 觉得很有意思在这做个记录, 题目如下:

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

示例 1：

输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。
1.  1 阶 + 1 阶
2.  2 阶

示例 2：

输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。
1.  1 阶 + 1 阶 + 1 阶
2.  1 阶 + 2 阶
3.  2 阶 + 1 阶

• 第一次尝试

像我这种算法低能儿, 第一个想到的无非就是暴力算法了, 顾名思义就是利用排列组合的思想将所有的组合利用递归, 循环等手段一个一个列举出来, 代码如下

public class Solution {
    public static long climbStairs(int n) {
        return move(0, n);
    }

    public static long move(long start, long end)
    {
        if (start > end) return 0;       // 起点大于终点, 没有路径

        if (start == end) return 1;      // 起点等于终点, 只有一条

        long sum = move(start + 1, end) + move(start + 2, end); // 递归
        return sum;
    }
}

但是当我兴高采烈的将代码提交之后, 悲剧发生了, 暴力算法这一次并没有那么的好用.

发现只通过了21个测试用例, 执行到44的时候时间就不够用了, 那么到底花了多少时间呢, 让我们自己来测一下, 在原来的代码上添加测试代码.

 public static void main(String... args)
 {
     long start = System.currentTimeMillis();
     System.out.println("有 " + climbStairs(40) + " 种走法.");
     long end = System.currentTimeMillis();

     System.out.println("耗时: " + (end - start) + "ms");
 }

执行测试用例 44

发现花了7秒多, 再来试试 41

发现只花了1秒多, 仅仅相差3个台阶, 时间却有6秒之差, 暴力算法的报应终于来了, 数学中这种现象称为指数爆炸, 由于使用了暴力枚举, 算法的时间复杂度是指数级上升的, 当台阶数达到指数爆炸的零界点时, 灾难就会发生

让我们来画一个递归树, 可以更加清晰的意识到这一点.

这是一颗4层楼梯走法的递归树

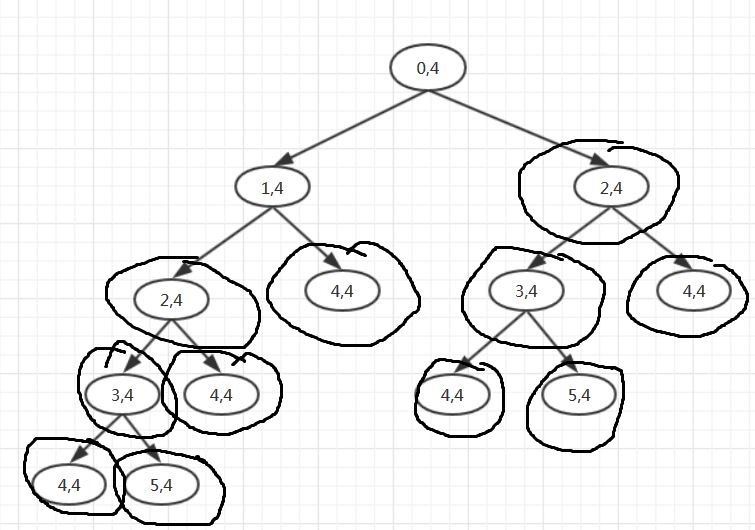
注意画圈部分, 可以发现,  递归树在生长时有大量的重复节点, 重复率高达90%, 到这里你应该能理解为什么会出现指数爆炸这种现象了吧, 当基数越大时, 递归树生长的也就越大, 重复计算的节点也就越多最终会导致指数爆炸。

既然定位了问题的所在, 那么就来考虑一下如何解决, 针对于重复数据的情况, 我们可以考虑使用备忘录的思想来优化我们的算法。

• 第二次尝试

    public static long climbStairs2(int n) {
        Map cache = new HashMap<>();        // 使用哈希结构缓存(查找快速)

        return move(0, n, cache);
    }

    public static long move(long start, long end, Map cache)
    {
        if (start > end) return 0;       // 起点大于终点, 没有路径

        if (start == end) return 1;      // 起点等于终点, 只有一条

        if (cache.containsKey(start)) return cache.get(start);     // 缓存中有的话就不需要递归了

        long sum = move(start + 1, end, cache) + move(start + 2, end, cache); // 递归

        cache.put(start, sum);          // 缓存起来

        return sum;
    }

增加一个 Hashmap 来作为我们的备忘录, 再来测试一下, 测试代码不变, 执行测试用例 44。

缓存的效果很明显, 由于缓存了大部分的数据, 重复计算的次数,递归层数大幅减少, 再来测一个大的, 执行测试用例 4400

即便将测试用例扩大100倍, 也不过只花了 10ms 而已, 回去提交我们的代码。

当然这并不是这道题的最优解, 我们优化这道题的核心思想是用空间换时间, 还是有一定的弊端的, 这道题的解法还有 动态规划, 斐波那契数, Binets 方法等等优秀的算法, 感兴趣的同学可以自行的去了解一下, 但切记不要走火入魔了, 算法只是为了解决问题, 过度的追求效率, 反而会得不偿失。(溜了溜了.. 脑壳痛)